Home About us Contact us Protuner Loop Analyser & Tuner Educational PDFs Loop Signatures Case Histories
Michael Brown Control Engineering CC
Practical Process Control Training & Loop Optimisation
CONTROL LOOP CASE HISTORY 147
WHY BASE-LAYER FEEDBACK CONTROL IS NEEDED
A friend of mine was appointed to start an advanced control and optimisation group in a very large chemical plant and he hired a group of academically highly qualified young APC (advanced process control) engineers mostly not long out of university. Most of them were extremely bright, but had little field experience. They argued that with the wonders of modern APC techniques and software the base-layer control system was unnecessary. My friend asked me to come and give a course on practical feedback control to the group.
At university generally when studying control everything is based on perfect mathematical models, and as everyone who has studied feedback and advanced control knows, the modern control systems can deal perfectly with such ideal models. I personally never cease to wonder at the genius of the mathematicians who came up with the theory behind feedback control.
In the real world of industrial control there are many problems. The dynamics of actual processes are seldom perfect models, and can often be more complex than simple first order models which are used on most tuning methods. The models themselves are also not constant and can change quite drastically for a variety of reasons. They are often not linear. On top of that there are often problems with components in the control loop including for example measurement problems, difficult processes like slurries and acids, and the greatest problem of all, the final control element, the valve.
The valve is generally a mechanical device subject to all the problems that can affect moving parts. There are pressure variations, corrosion, and abrasion, rangeability, installed linearity, hysteresis, positioner problems, friction, backlash, and sticking to name a few. The control system, be it a feedback controller or direct APC, sends a signal to the valve, and this signal in actuality is instructing the valve or any final control element, to pass a certain quantity of product (for example steam, a gas, or a liquid) into the process to change the measurement to the desired setpoint.
This is where the problem comes in. If the valve did comply with that then I would agree that there would be no need for a base control layer. However in real life, valves seldom give a result the controller is wanting, and this is why a feedback control layer is absolutely essential. The APC then sends the signal to the setpoint of the feedback controller, and this is the device that ensures that the valve does in fact pass the correct amount of product into the process.
In reality it is absolutely amazing how well a properly optimised feedback control system can overcome valve problems to achieve this.
A lovely example of this is given in this article of a control loop which is controlling the top pressure of a distillation column in a petro-chemical refinery. This control is absolutely essential to the performance of the tower, and it had been causing the operators a huge amount of problems, as it cycled around with quite a large variance, and was adversely affecting product quality. Many attempts had been made to tune the controller better, but with little success. It was hoped that if we could improve the loop performance then the loop could be incorporated into the plant’s APC system.
Fig. 1
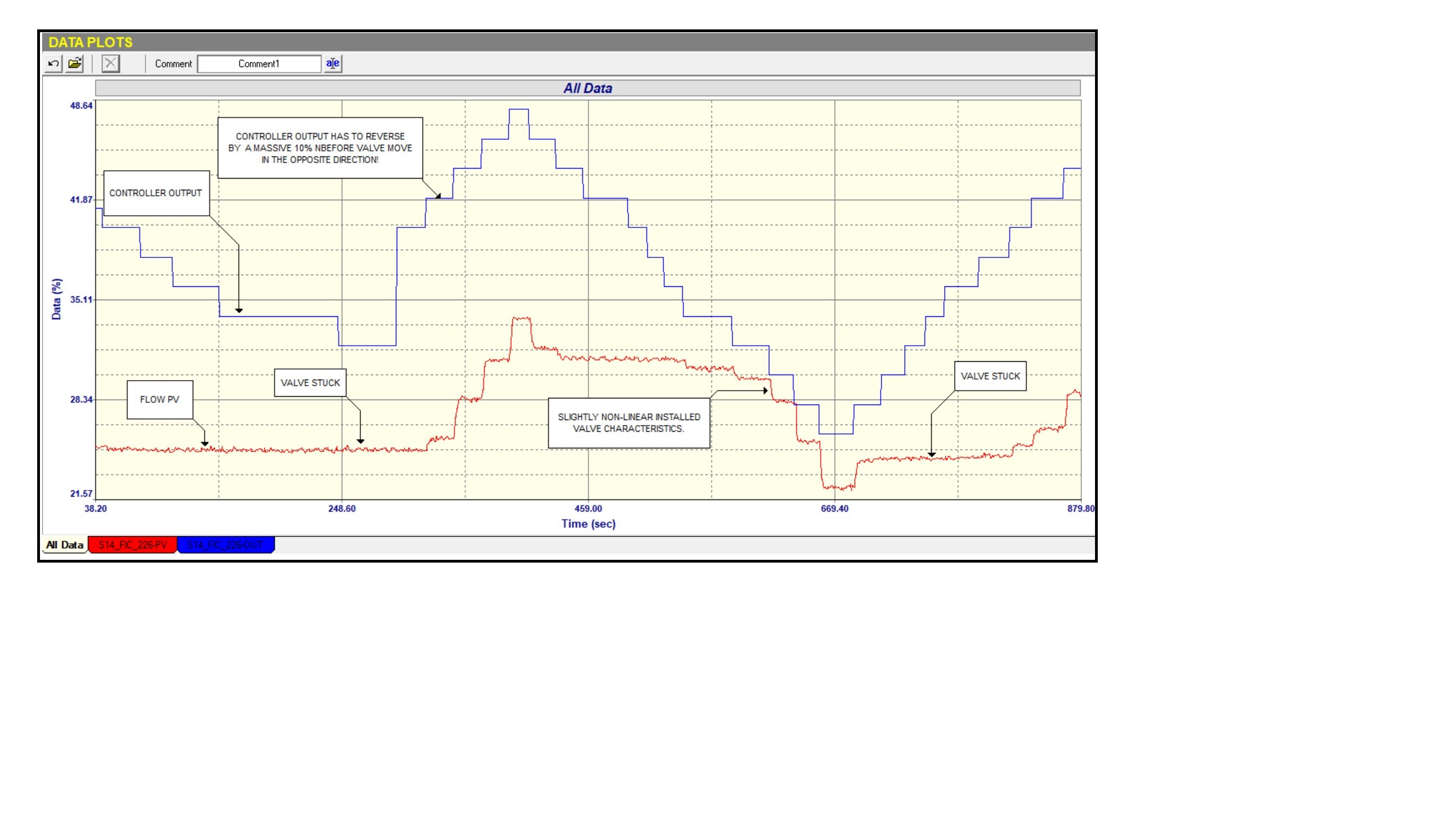
Figure 1 is a section of the open loop test performed on the loop, where the controller is placed in manual, and step changes made on the output of the controller. The figure shows two interesting things:
The first is that the process is an integrating process with an initial first order positive lead, which is a rather unusual dynamic, and it is extremely difficult to tune if you have not received the correct training to understand it. Integrating (or ramping) processes are like levels where you have to balance the incoming and outgoing flows if you wish the process to remain constant. For example in the case of a level if the incoming flow into the top of the tank is larger than the flow leaving the tank, then the level would ramp up at a constant ramp rate until the tank overflowed.
Integrating processes like levels are very different from “self-regulating” processes like flow control and are tuned in a completely different manner.
In this case this particular process also exhibited the lead which can be seen in the figure as the initial fast rise in the pressure before the pressure starts ramping at a constant rate. This is a very interesting phenomenon because in actual fact when the step change is made the process starts out as a self-regulating process but then changes into an integrating process. You always tune a process the way it starts, so in this case it is tuned on the initial response as self-regulating.
The second thing is that the figure also displays large hysteresis on the valve. This is a problem that you see when you reverse the valve. Typically if the valve sticks or has backlash, then one needs to increase the output of the controller considerably past the point where it at was before you reversed the valve. Figure 2 shows how valve hysteresis can be measured.
Fig. 2
Unfortunately integrating processes which this falls under in the long term are also subject to all sorts of problems which can often induce continuous cycling. Many of these problems are caused by valve problems, particularly hysteresis. Usually if you have hysteresis on integrating processes you cannot avoid continuous cycling.
In this case however the initial lead saves the day. It is extremely fast and reacts so quickly that with good fast tuning, and although the output of the controller is in a continuous cycle to get the valve to the right balance position the process remains absolutely stable.
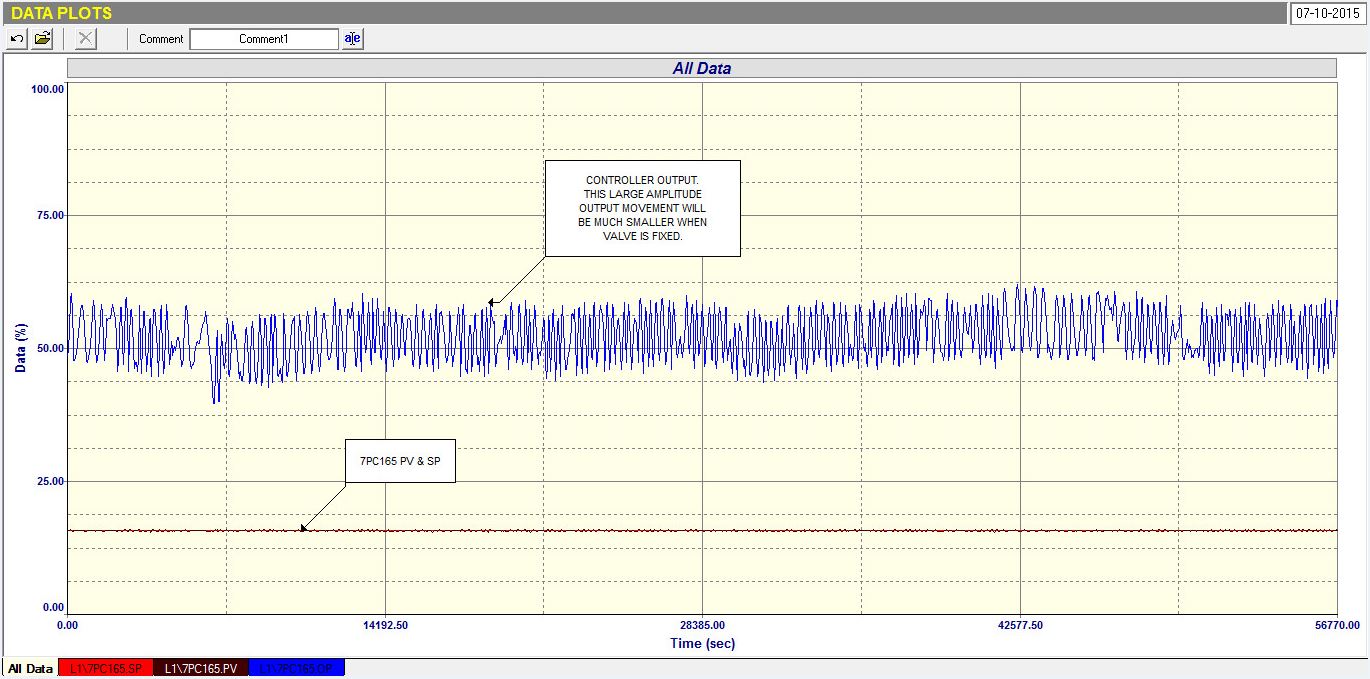
Fig. 3
Figure 3 shows a test with the final tuning recorded over 16 hours showing how the controller output is cycling in a 10% band (because of the hysteresis), but the process sits exactly on setpoint even with the load changes that were occurring form time to time which can be seen by movement in the average value of the output.
This to me is one of the most incredible tests I have witnessed and it shows how powerfully feedback control can overcome severe problems. It would have been impossible to try and control this pressure directly from the APC. The pressure would have been cycling all over the place.
For interest sake the original tuning was:
P = 2.0
I = 0.2 minutes/repeat
D = 0.35 minutes
The new tuning as given by the Protuner loop analytical and tuning software was:
P = 14.0
I = 1.3 minutes/repeat
D = 0 minutes
As mentioned earlier very few people know how to tune this type of process, and it can be seen how bad the original tuning was.