Michael Brown Control Engineering CC 

Practical Process Control Training & Loop Optimisation

LOOP SIGNATURE 11

 

 

DIGITAL CONTROLLERS – PART 3
The P Term

 

 

Figure 1 shows a simplified P only controller.  The P term may be considered as a pure amplifier that multiplies the input error signal by whatever gain (Kp) is set in the controller to produce the controller’s output signal (PD).  The bias allows the output to be manually adjusted either up or down between 50% and 100%.

Figure 2 shows a recording of a test on a P only controller with Kp = 4, with the controller mounted in the test rig as described in Part 2 of this series.  A setpoint (SP) change of 10% has been made, which gives a step change of error of 10%, and the PD has immediately stepped up by 40%.

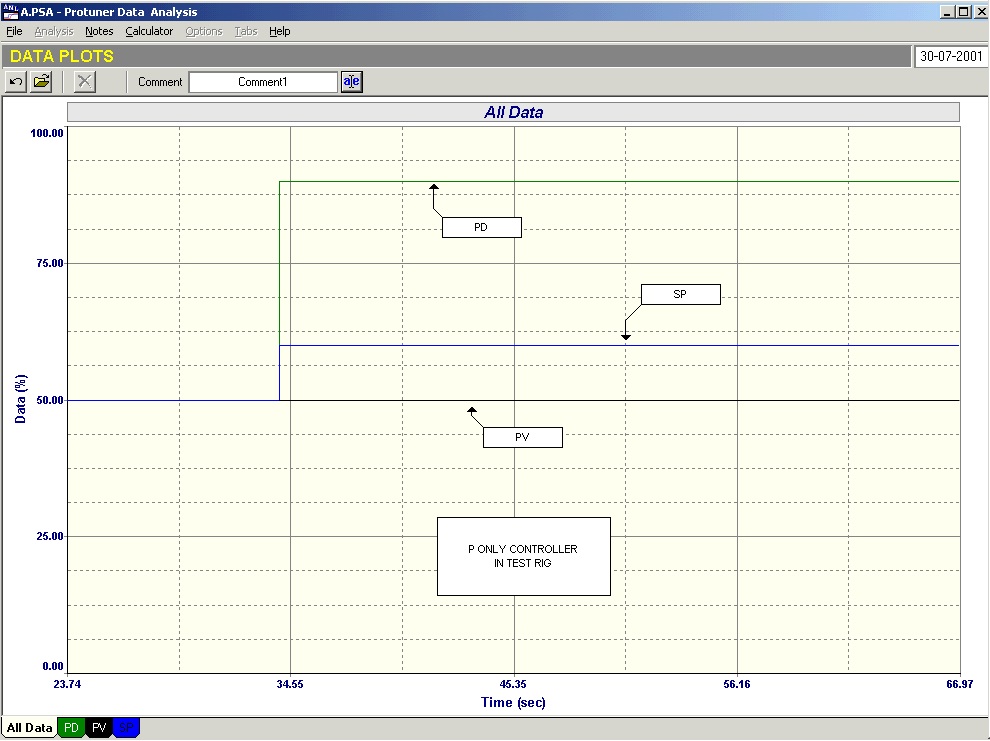
As there are no standards in PID controllers, manufacturers use various units for the P term.  Probably the most common is “gain”, which as mentioned above is the amplifying factor, and is defined as the size of the output step divided by the size of the input step.
Another term used by quite a few manufacturers is “proportional band”.  The relationship between gain and proportional band is:

Proportional Band = (1/Gain) x 100 %

Proportional band is sometimes a useful concept in aiding one in explaining controller responses, as it may be considered as a graphical representation of the control range. 

This is illustrated in Figure 3, where a gain of 2 has been entered in a P only controller.  The proportional band works out at 100/2 = 50%.  This can be drawn as a band of 50% width lying around the setpoint.  Note that the band need not be equidistant around the setpoint, but can in fact move around the setpoint.  However in ordinary controllers the band normally can never move away from the setpoint.  (The position of where the setpoint lies within the band is in fact set by the value of the bias).

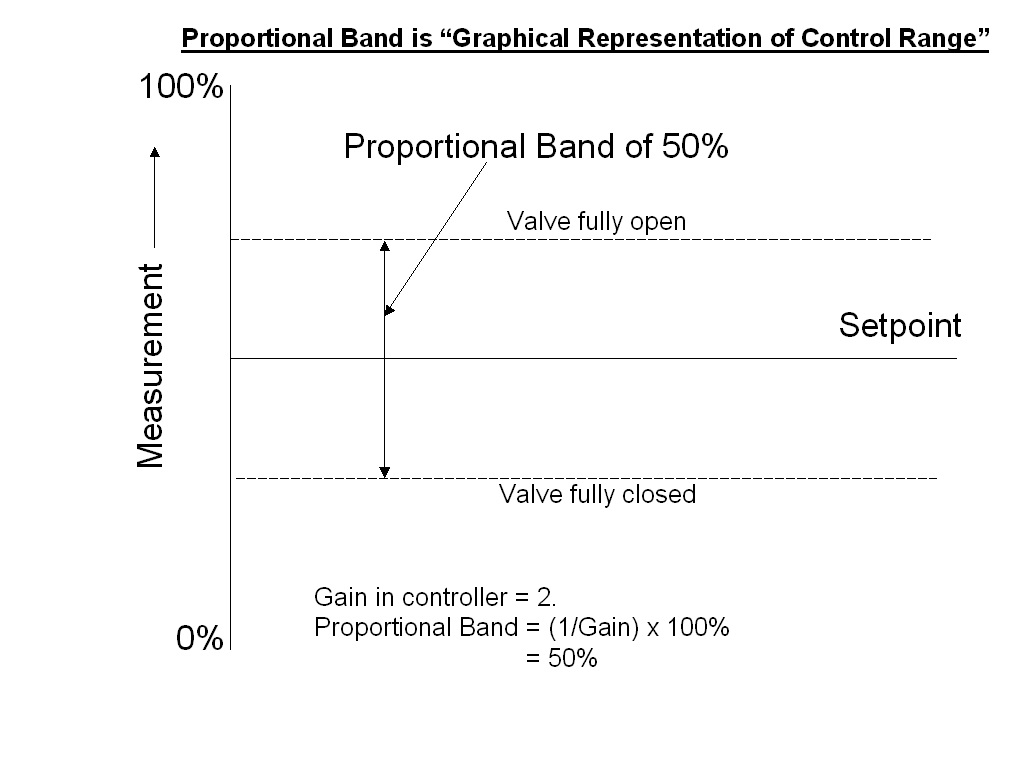
Assume that at a particular moment of time the PV value was sitting on the bottom edge of the proportional band.  This would mean that at that time the valve would be at one of its extremities, either fully open or fully shut.  If the measurement were then to move up to the top of the proportional band, then the valve would have moved through its range to the opposite extremity.

Thus the proportional band represents the control range, as control can only be achievable between the two valve extremities.
 
This leads to an interesting thought.  In the first article in this loop signature series, it was mentioned that control performance or variance is a measure of error effectively totalised over a period of time.  If we were able to put more gain into a controller and make the proportional band narrower, then it is feasible to believe that the variance would improve, as errors should be smaller in a narrower proportional band.  Therefore the smaller the band, the better the variance, provided we could in fact achieve control within that band.
 
Taking this concept to a ridiculous extreme we could speculate that if we were to put an infinite gain into the controller, and make the proportional band infinitely small (i.e. zero), then we should have zero variance, as there should then be no control error.  Infinite gain is of course ON/OFF control, and as we know, ON/OFF control is in fact in a continuous cycle, either switching the final control element fully on or off, as the PV rises and falls through setpoint. This results in very poor variance.

In reality as the gain is increased in the controller, the loop will eventually start reacting to changes in setpoint or load with a cyclic response, and this will get worse as the gain is increased.

Therefore for minimum variance there is a balance between the amount of gain we can insert in a controller, and the amount of cycling that we would be prepared to tolerate in any particular control loop.  The actual limit in practice would be where the gain in the controller would give rise to a quarter damped amplitude response on a step change in setpoint.

To explore the limitations inherent in a P only controller, take the practical case of such a controller that is often still encountered in level controls in plants.  This is the ball valve. 
The ball valve and level process make up a complete feedback control loop.  The ball is the measuring element.  The arm connecting the ball to the valve is the proportional control mechanism, and the valve the final control element.

Imagine the system illustrated in Figure 4 is being used for controlling the level in the reservoir feeding water to our plant.  When we come to examine the system, let us imagine that we find that the inflow and outflow are equal.  The level is therefore constant at some particular point.  Let us call this point our desired level, the setpoint.  We then proceed to perform a little experiment, and open the manual valve controlling the flow of water to our plant by 10%.  As the valve opens, the flow increases and the level starts dropping.  As it does so, the ball drops with it and opens up its valve, which in turn increases the flow of inlet water.
 
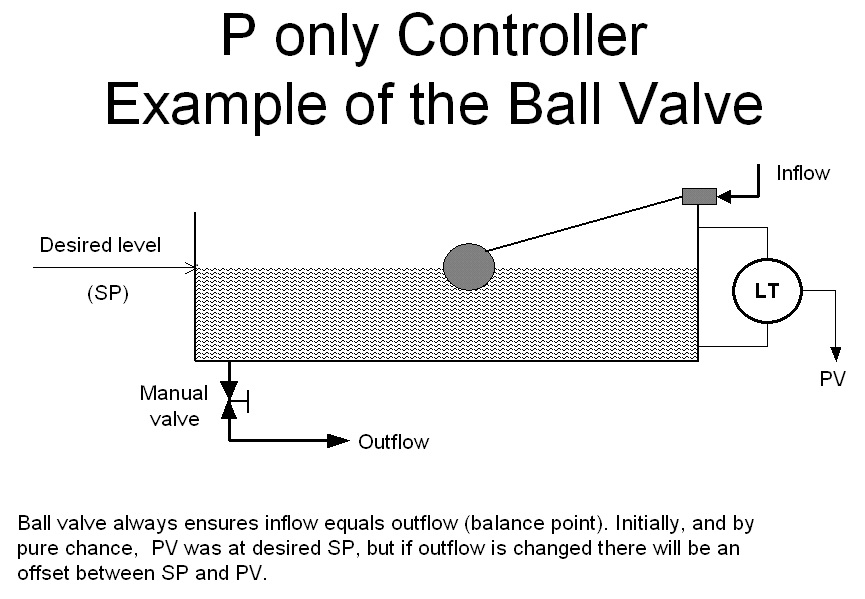
Eventually the inflow will equal the outflow at which point the level stops dropping, and will remain constant.  The control system is now in equilibrium, and the level will remain at the new value, as long as no further changes are made to the manual valve. 
The level is again under control, but is no longer at setpoint, and we say that we are now controlling the level with an “offset”.

Offset is the main drawback to P only control.  There is nothing in a P only controller that can do anything to permanently eliminate the offset.  For practical purposes one can generally assume that a P only control system will almost definitely control with offset at some stage or other.
In certain instances one can tolerate a certain amount of offset.  However the majority control loops are there to keep the process at the setpoint.

The best one can do with a P only controller is to minimise offset.  This can be achieved in two ways.
 
Firstly if the controller gain is increased, the offset will decrease proportionally.
 
Secondly, one can bring the process to the setpoint by adjusting the valve position manually.  In the example of the ball valve above, one could physically bend up the arm between the ball and the valve to allow the level to come back up to the setpoint.  In a real controller the same effect can be achieved by adjusting the bias.  This adjustment is often called “manual reset”.

The problem with manual reset is that if you had reset the offset at a particular point in time, then when changes occurred in the process again, another offset would result.  In practice, manual reset is used only for initially setting up P only control systems.

In the real world of industrial process control, P only control should only be used on processes that are tuned with a large P gain value.  It would generally be impossible to use it where the P value is small, as large offsets could result.  Therefore one normally only finds P only controllers on integrating loops such as level controls where high controller P gain is normal.

Integrating loops are in actual fact better without the I term in the controller.  There are two reasons for this.  The first is that as mentioned in previous articles, any hysteresis on a valve on an integrating process that is controlled with P+I control will result in continuous cycling. The second reason is that the I term introduces a second integral term into the combined loop process transfer function, and prevents perfect pole cancellation tuning from being achieved.

Therefore the only reason that one should technically ever use the I term in the controller on an integrating process, is if the possible offset is unacceptable. However, in reality, most people don’t like processes being controlled with offset, even if it is actually acceptable, and as a result one finds that the I term is used on most integrating processes.