Home About us Contact us Protuner Loop Analyser & Tuner Educational PDFs Loop Signatures Case Histories
Michael Brown Control Engineering CC
Practical Process Control Training & Loop Optimisation
LOOP SIGNATURE 12
DIGITAL CONTROLLERS – PART 4
The I Term
In the previous article in this series, it was shown that the main problem with the P only controller is the fact that it is not capable of eliminating offset between setpoint and process variable (PV) by itself. Manual reset was discussed whereby the user can manually eliminate the offset by adjusting a bias added to the process demand (PD - output signal from the controller). This however is a short-term solution, because another offset will arise if a load change occurs.
A mathematical genius in the 1930’s found a simple way to overcome the offset problem, by introducing an automatic mechanism to eliminate offset. This is the I or “integral” term. Figure 1 shows how an integrator works. The error signal is fed into the input of the device. If the error is zero the output of the integrator remains fixed at whatever its current value is. However if an error does appear at the input, then the unit starts integrating the error value with time. Thus if the error input is a step, as shown in the figure, the output of the integrator will be a ramp, the slope of which will remain constant for as long as the error remains constant. If the error input is a larger step (bigger error) then the ramp will have a proportionally steeper slope. (It is important to note that the integral action in a controller is therefore greater, the larger the error. Conversely, as the PV gets closer to setpoint, so the integral ramp rate, and hence effect on the PD, will be much less.)
Figure 1.
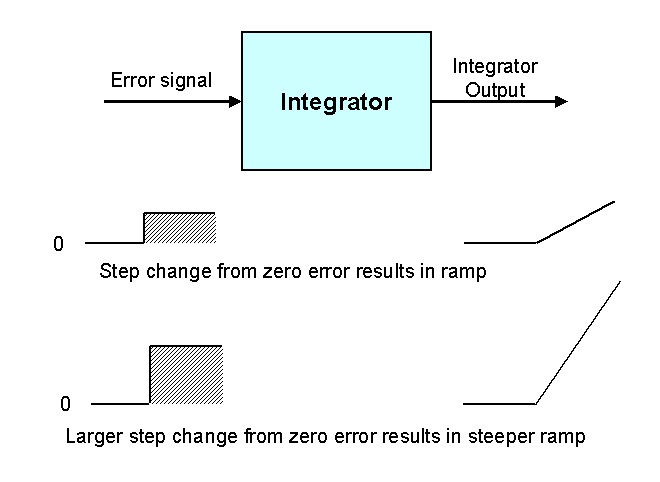
The integrator acts as an automatic offset adjuster, because if any error arises on its input, it will try and move the output in a direction to diminish the error. As the error gets smaller, then so will slope of the output ramp. When the error finally disappears, the integrator’s output will remain constant at its last value. Thus it acts as an automatic bias to eliminate offset.
It should be noted that the I term’s only purpose is to eliminate offset.
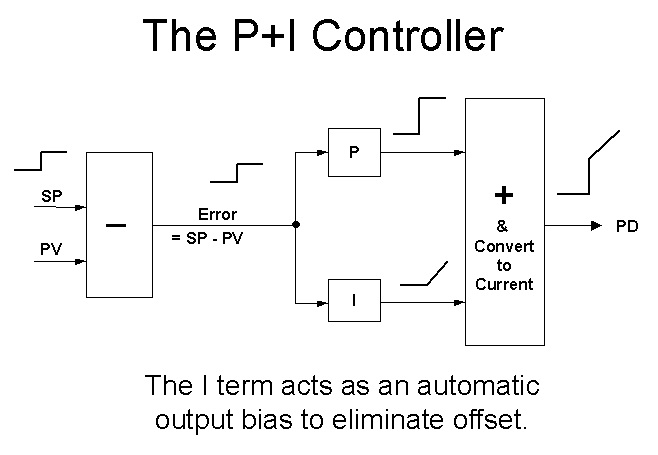
Figure 2 illustrates a simple P + I controller which is being tested. (See earlier article in this series for controller test procedures). A setpoint step change is made, which results in a step change in error appearing at the input of both the P and I blocks. The output of the P block is a step, and the output of the I block is a ramp. The two responses are added as shown in the figure, so that the PD is a step followed immediately by a ramp.
Figure 2.
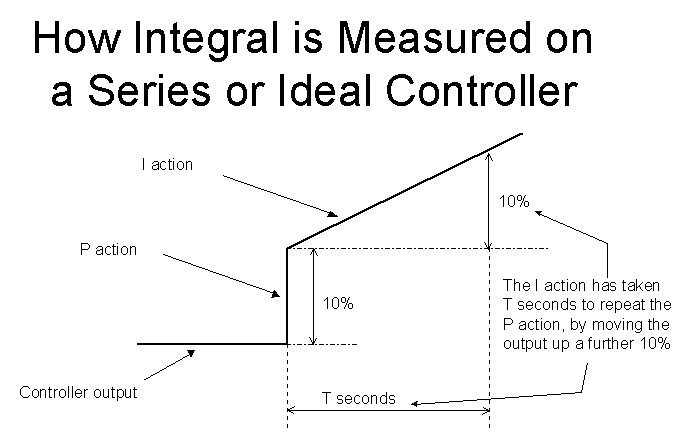
This response is enlarged in Figure 3. Imagine that the step portion of the response, which is the contribution from the P block, has a magnitude 10%. The I term then carries on increasing the PD at a constant ramp rate. If it takes say T seconds to raise the output a further 10%, it is said that the I’s contribution has “repeated” the P’s contribution in T seconds.
The most commonly used units of measurement of the I term are seconds/repeat, or minutes/repeat, or the inverse, which is repeats/second, or repeats/minute. As usual there are no standards, and each controller manufacturer use whatever unit they wish.
Note that these terms only apply to controllers with Series or Ideal algorithms. The time has now come to explain why the Parallel algorithm behaves so differently.
In the earlier article on algorithms it was mentioned that if one is to reduce the gain on controllers with the Series or Ideal algorithms, the process response to a step change would be slower. However, conversely on a controller with the Parallel algorithm, the response would become more cyclic.
The algorithm for the Parallel controller with P + I tuning is:
Output = KP + 1/TIs
The algorithms for the Series or Ideal controllers with P + I tuning are the same. (They differ only in the D term, if it is used):
Output = KP (1+ 1/TIs)
It is important to note that in the latter algorithm, the P term also multiplies through into the I term, so if Kp is reduced, then the integral becomes slower, and the slope of the ramp is less.
Figure 3
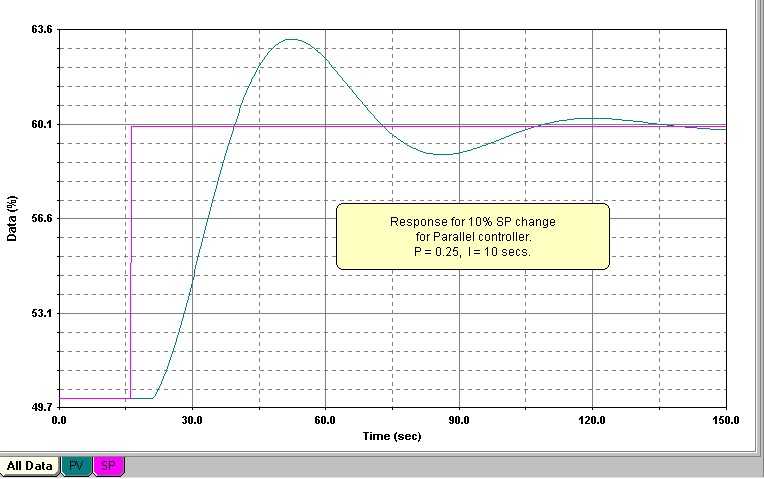
The top graph in Figure 4 shows the response of a P + I controller undergoing testing. The controller gain Kp = 1. The I is set to a value that on the Ideal and Series controllers would repeat the P action in T seconds. It should also be noted that a Parallel controller would also have an identical response to this for Kp = 1 and with the same I value.
Now in the Parallel controller, if the gain was halved (Kp = 0.5), then nothing would happen to the integral ramp rate as the two terms are not linked at all. Therefore on a 10% step change in error, the P action would result in an output step of 5%, and the integral would still continue ramping up at the same rate as it did in the previous test with Kp = 1
Figure 4.
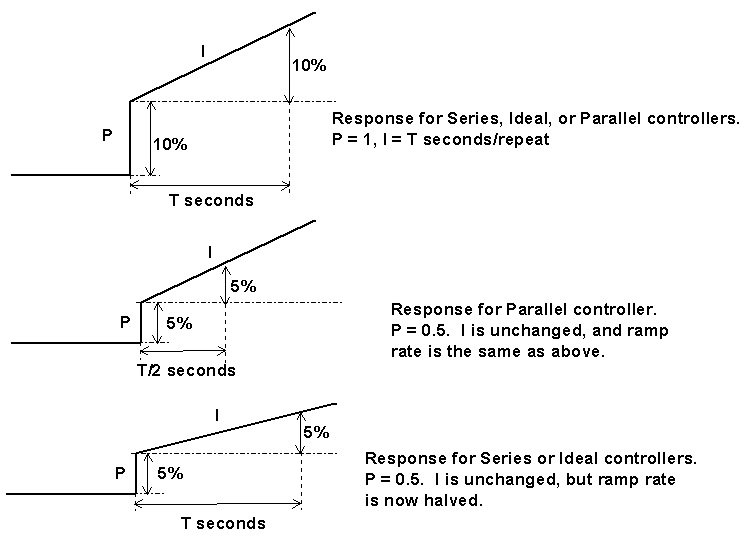
This is shown in the middle graph in Figure 4 It is now observed that the P action is repeated in time T/2 seconds. Therefore the reason that the Parallel controller gets more cyclic when the gain is reduced, is because effectively the integral gets faster in relation to the P action.
In the Series and Ideal controllers where Kp is multiplied with the I term, the integral ramp rate is now reduced by 50%, and as can be seen in the bottom graph in Figure 4, I repeats the P action in T seconds. Thus the relationship between P and I is maintained.
Figure 5.
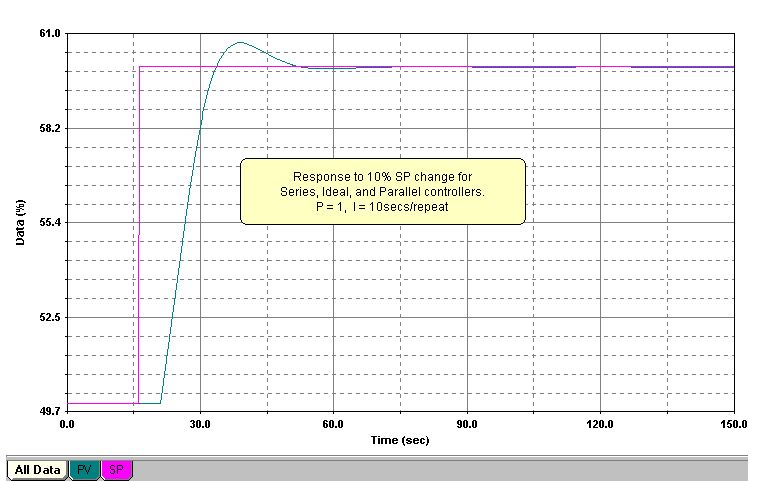
The difference between the closed loop responses of Series and Parallel controllers controlling the same process with a reduction in the gain, but no change in integral, is shown in Figures 5, 6, and 7.
In Figure 5, the response for any of the three algorithms is the same provided Kp = 1.
In Figure 6, the response for the Series or Ideal is shown with Kp = 0.25, and the Parallel in Figure 7, also with Kp = 0.25.
Figure 6.
Figure 7.
Whereas the response on the former has become very slow, the Parallel has become much more cyclic. This means that if one was using the Parallel algorithm and did indeed wish to reduce P by a factor of 4 to slow the response down, then you would also have to increase (lengthen) the integral by the same factor.
Thus the Parallel algorithm makes life extremely difficult for the poor instrument specialist, as tuning is made very much more complicated, as one has to adjust all the parameters simultaneously. On the Series or Ideal algorithms on self-regulating processes, once you have got the correct I (or I + D) settings, then you can leave those terms alone and play only with the P “knob” to obtain the desired response.
As mentioned in a previous article in this series, I have found that people who were “wizards” in tuning in their plants when they worked on older controllers, lost their “art” completely when newer computerised controllers were introduced which have the Parallel algorithm. This is because there is a completely different “feel” to the tuning.
Fortunately there was such resistance from users in the early days of computerised control systems with the Parallel algorithm, that manufacturers generally now offer the user a choice between the Parallel, and at least one of the others.
I would strongly recommend that you choose either the Series or Ideal. It will make your life very much easier when it comes to tuning.
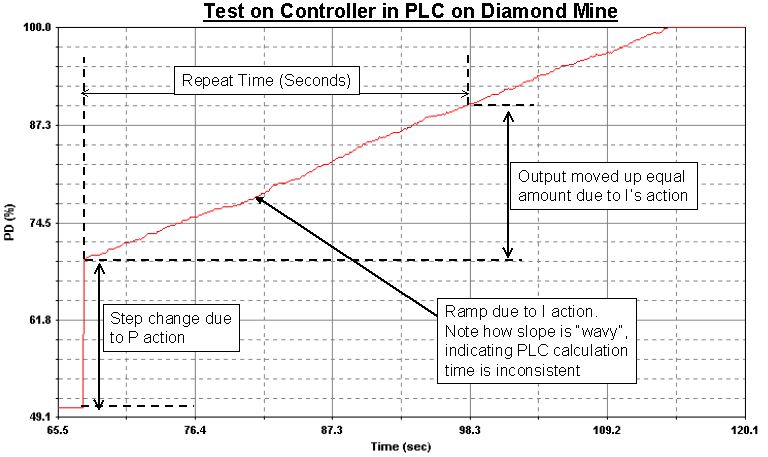
At the time of writing this article I was doing some optimisation on a very remote diamond mine in Southern Africa. The mine has standardised on a particular make of PLC for all its controls. Generally as PLC’s sometimes do not handle PID’s well, I always do some tests on them to check on the operation. In this mine we tested three PLC’s all of the same model on different plants, and found that they were all reasonably accurate with the P action. However they all had huge errors on the I timing response. The errors ranged from –50% to +50%. (The D response was not tested).
As the I function is completely time dependent, the problem obviously arises from the scan rate of how often the PID is executed in the PLC. Unfortunately the manuals on the PLC’s were really terrible with extremely poor, limited, and confusing descriptions of the PID operation. Also the plant personnel did not have any training on the PID operation. Therefore it was impossible to say whether the problem was a manufacturing error or faulty programming.
The scan rate itself as actually measured on the controller’s output was very different to the setting in the controller’s programme in the PLC, and did not tie in with any of the information given in the manual. The manual did however mention that PID block should be executed in a sequence free from interrupts.
Figure 8 shows one of the actual tests performed on the controller to check the P + I performance. It can also be seen in the test how the integral ramp is very “wavy” which would indicate possible interrupts upsetting the PID timing execution.
The mine is now going to go back to the supplier to get help and more explanations on why the controllers are not performing properly, and as to why they are so far off specification.
Figure 8.