Home About us Contact us Training Optimisation Services Protuner Educational PDFs Loop Signatures Case Histories
Michael Brown Control Engineering CC
Practical Process Control Training & Loop Optimisation
Loop Problem Signatures No 20
Filters - the great deceivers
Noise on the PV signal was discussed in the previous loop signature article, and it was mentioned that it is generally better to live with the noise rather than filtering it out; provided it does not cause the final control element to jump around excessively. This article explains this reasoning.
Normal filters used in process control have a first order lag type dynamic, which is generally preferable to time averaging filters. This is because PID controllers can handle lag dynamics better. A lag type filter is also referred to as a low pass filter, as it passes the lower frequencies and attenuates higher frequencies components. Visually the filtered signal appears to have less noise. Obviously the greater the filter constant, the smoother the output signal.
In the old analogue days filters were extremely difficult to implement, and as a result were seldom used. Today it is extremely easy to implement a simple lag type filter on a digital control machine. Only a few lines of code are needed. Most DCS, and a few PLC manufacturers offer filters as a standard block. These filters usually allow one to insert lags in a loop ranging from fractions of a second to literally hours.
When a filter is used in the control equipment it is usually inserted before the controller and the Operator's display, or SCADA.
Figure 1 shows the response of a flow signal to a step change on the PD (controller output).
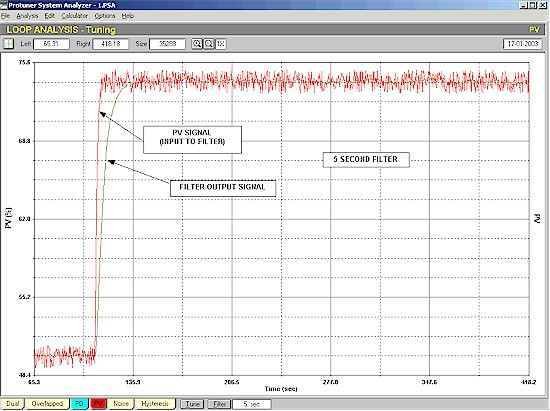
Figure 1
The signal has noise of some 2% amplitude on it. The signal is then passed through a filter with a 5 second time constant, and the output of the filter is shown in the same figure superimposed over the original PV signal. It can be seen that the noise amplitude on the filtered output has been reduced considerably. There are still some fluctuations due to the lower frequency components present. Apart from that, the signal has not been changed drastically.
In Figure 2 one can see how the situation has changed when a 50 second filter is used.
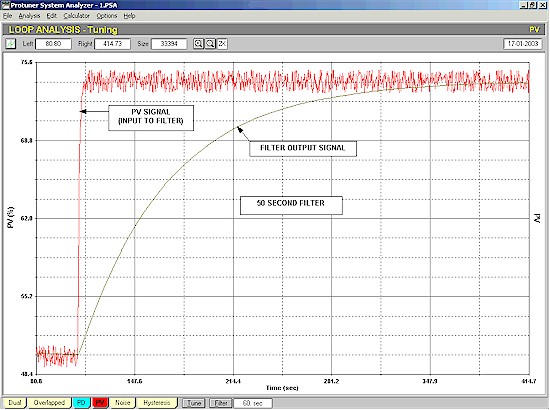
Figure 2
The noise has now been completely eliminated. The filter has certainly achieved its purpose insomuch as it has got rid of the noise. However the signal response has been really drastically slowed down. The filter has now replaced the flow process as the dominant dynamics in the control loop. In other words we are now trying to control a filter rather than a flow!
Many learned texts on control have stated that if the time constant of the filter exceeds the dominant time constant of a self regulating process the control will be adversely affected. This is not necessarily correct, as you will see in the next example. Tests we have performed show that you can in fact get quite reasonable control on loops with relatively heavy filters. However there are other really serious effects which are more important, and which make the use of big filters very undesirable.
One of these seriously bad effects is that filters can cause excessive PV overshoots (as high as 300%), on step-changes in setpoint. Such an overshoot is shown in the next example.
In previous articles I have also referred to filters as the world's biggest liars, as they can distort the response of the process as seen on SCADA or DCS screens by the operator. The filter actually tends to reverse the facts, making good things look bad, and bad things look good!
To illustrate this point, Figure 3 is the recording of a control system on a noisy process.
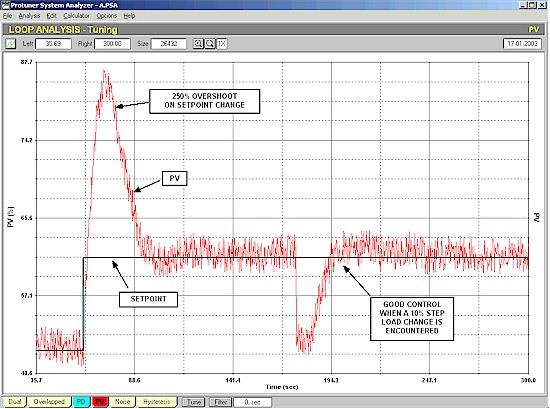
Figure 3
The controller has a filter with a 50 second time constant in it. The controller is extremely well tuned. The recording is made with the Protuner analyser connected at the input to the controller (upstream of the filter). A 10% step change in setpoint is followed by a 10% step change in load. An enormous overshoot on the PV response to the setpoint change can be seen. It is really bad. The load change however is controlled well. The controller brings the process back to setpoint speedily with little overshoot. This is in fact really good. (It also shows you can indeed get quite good control even with a big filter.)
Figure 4 shows what the Operator sees on his screens with a filtered signal.
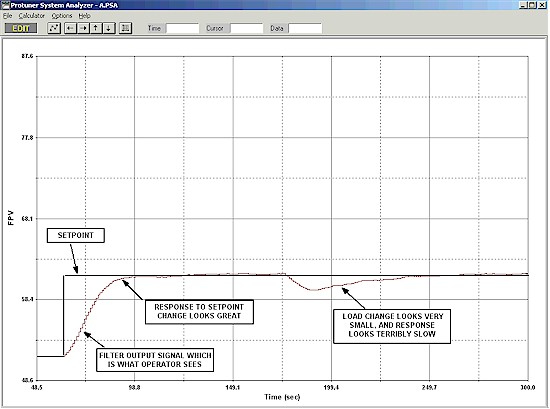
Figure 4
The setpoint change looks really good. There is no sign at all of an overshoot. However the load change now looks terrible. It only shows as a tiny offset, which seems to take forever to get back to setpoint. Therefore the filter has completely distorted and reversed the true facts. This is to me the most dangerous thing of all, as the
Operator doesn't really know what is going on in the plant.
It must be remembered as well that the people doing the tuning are generally also unaware of what filters can do, so they often ruthlessly eliminate noise with enormous filters, and then do tuning whilst looking at the filtered signal, so they have no real idea of the true response.
It is common practice these days for management to use the information available on the SCADA for management evaluation and control purposes. Therefore it is vital that people should avoid using big filters if they want to have reliable information. This was illustrated on a mine in Southern Africa where all the plant accounting and management information was based on a transfer from their SCADA package into spreadsheets. Large filters were applied on nearly every loop. It was a continuous source of puzzle to the Metallurgists as to why the plant balances never seemed to work out.
Rules for Filtering
Sometimes one has to apply filters when the noise is too much and starts moving the final control element around too much. If you apply the following "rules of thumb" you will find that you can't go too far wrong.
- If possible, eliminate the noise at its source.
- Use an anti-alias filter on the transmitter. (To be discussed in future loop signature).
- Try tuning without a filter and check at the actual valve if it is moving due to the noise.
- Avoid using a bigger filter than necessary.
- Biggest filter < 10 x (Process deadtime + Scan rate of controller).
- Use I-PD controller with filters. (See loop signature no. 16).
- Train the Operators and process people about filter effects.
The last point is one of the most important. Unfortunately process personnel are so used to heavily filtered signals in most plants, that they get very unhappy when filters are removed. As mentioned in the last loop signature, they mistake noise for instability. It is sometimes very hard to convince them that the control is now much better.
It was mentioned earlier that if you do have to use a filter, then it should be inserted in the control equipment rather than the transmitter. This is because you cannot see the control response at all if you filter in the field. The one exception to this rule is an anti-alias filter, which will be discussed in a future loop signature.