Home About us Contact us Protuner Loop Analyser & Tuner Educational PDFs Loop Signatures Case Histories
Michael Brown Control Engineering CC
Practical Process Control Training & Loop Optimisation
Loop Problem Signatures Part 2 - 18
DYNAMICS OF MORE COMPLEX PROCESSES
END POINT CONTROL (THE BATCH REACTOR)
The previous Loop Signature Article published two months ago dealt with the dynamics of integrating processes with large lags. In this article we will deal with a specific case of such a process, which is found when controlling setpoint changes in batch reactors. These are typically found in the following industries:
- Food.
- Brewing.
- Chemical.
- Pharmaceutical.
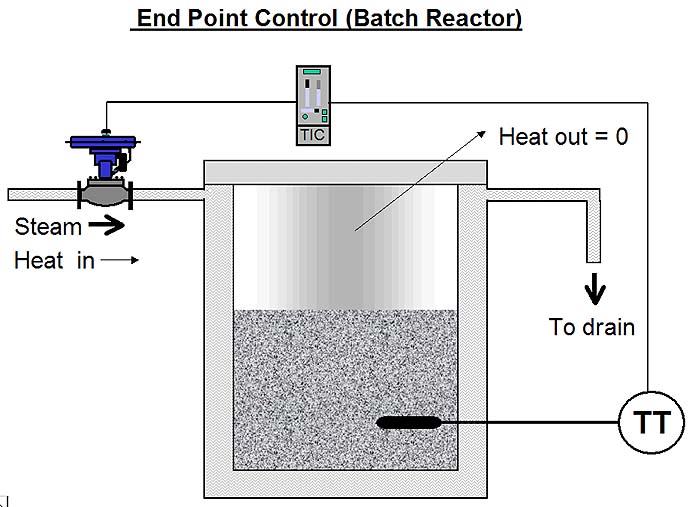
Fig. 1
Figure 1 gives a simplified diagram of such a unit as typically used in the pharmaceutical industry. Basically it is like a “cooking process”. A batch of product is placed in the interior of a hollow-jacketed stainless steel vessel. The product is to be heated by passing steam through the jacket. To do this the vessel is closed; the operator places the temperature controller in automatic, and changes the setpoint in a single step from the ambient to the cooking temperature. (In certain applications the setpoint may be ramped up at a preconfigured rate.)
The control object in the pharmaceutical industry where each batch can be worth huge amounts of money is to firstly get the temperature up to the cooking temperature as quickly as possible. The reason for this is that the heating-up takes quite a long time. The faster it can be done, the more production can be achieved.
Secondly, no overshoot of setpoint is allowed. This is because there is no cooling, and there is a relatively large thermal mass in the reactor, so if it overshoots, it will not cool down quickly, and the product will be ruined.
Now an apparent problem exists. The process is integrating. As mentioned many times in previous articles integrating processes are “balancing” type processes where one has to balance the input and the output of the process to keep the PV constant. In this case the process input is energy in the form of heat. However as discussed above, there is no cooling, so the heat coming out of the reactor is zero in the short term. This in turn means that the control valve has to be closed to maintain balance.
Therefore to reach final temperature without overshoot it means that the controller must allow sufficient steam into the jacket, and must then shut the valve completely before the temperature actually gets to setpoint so the temperature will finally stop rising exactly at setpoint. This sounds quite difficult.
This control problem is close to my heart, as I once spent a day and a half in a brewery trying to tune a controller on a similar process. This was right in the early days of my career in optimising, and I still had a huge amount to learn. I failed completely in this case, and was sent packing with “my tail between my legs”. Definitely not one of my more shining moments.
What I didn’t know is the following fact, which I try and drum into delegates attending my courses:
“If you use the integral term in the controller on an integrating process you WILL get overshoots
on setpoint step changes.”
(This is largely due to the slightly strange phasing relationship of phase lag when it comes to combining an integrating process with a controller with the integral term.)
Therefore the I term cannot be used in this application. This leaves the P and D terms. Obviously the P term is a must, but what about the D term? The answer to this was discussed in the previous Loop Signature article, and in the series of articles on the derivative term in the Part 1 Series of Loop Signatures (available on CD for users outside Southern Africa ). It was said the D term helps really improve control response on only two types of process dynamics. One of these is on integrating processes with long lags.
Batch reactors generally exhibit this type of dynamics, although I have come across a few that have negligible lags. However if they do contain a long lag, then this is where derivative really comes into its own and can drastically improve control response.
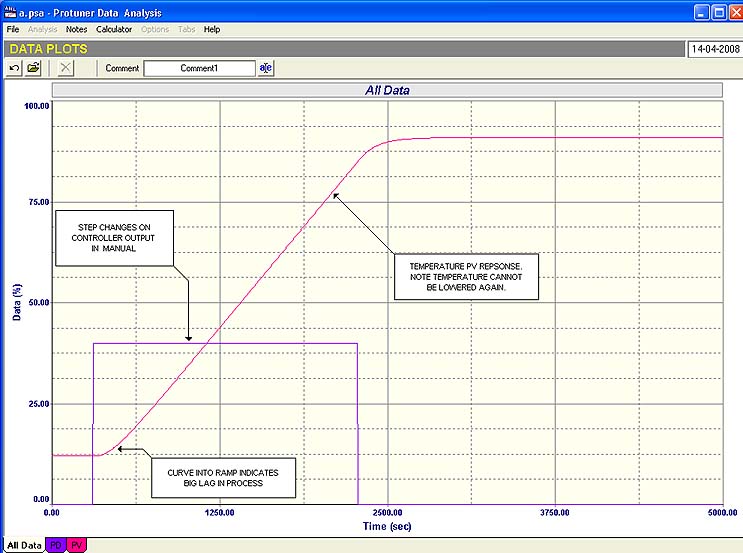
Fig. 2
Figure 2 shows the process open loop response to a step change in the controller’s output, firstly up, and then down. Three things are apparent from the test. Firstly it is a very slow process (with a very small process gain). Secondly a long lag is present, as indicated by the definite “curve up” into the ramp. Thirdly it is impossible to drop the temperature in the short term, as the balance point is with the controller output at zero, i.e. the valve is closed.
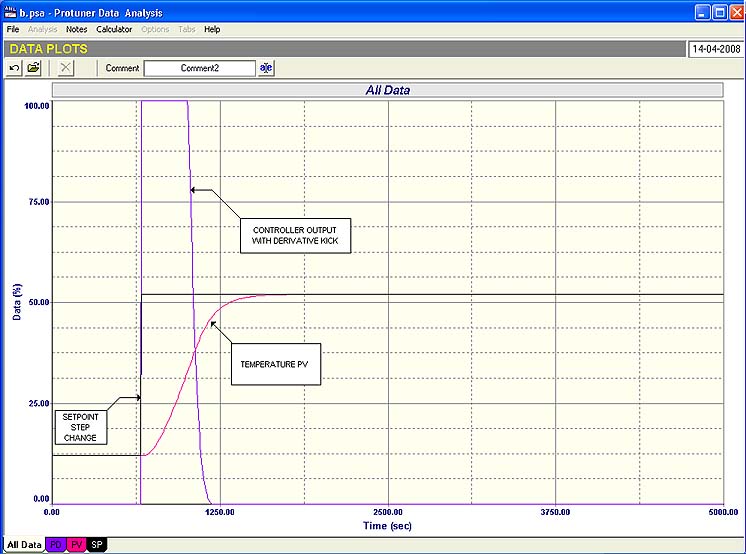
How does one then tune such a process to achieve the desired control objectives? Well two of the parameters are fixed. Firstly the I term must be switched off as we don’t want overshoot. Then secondly, as described in the previous Loop Signature article, the D term must be set equal to the time constant of the lag, to cancel it out. That finally leaves the P term, and this has to be tuned by trial and error, starting with a smallish value, and increasing it, so as to get as fast a response as possible without overshoot.
Fig. 3
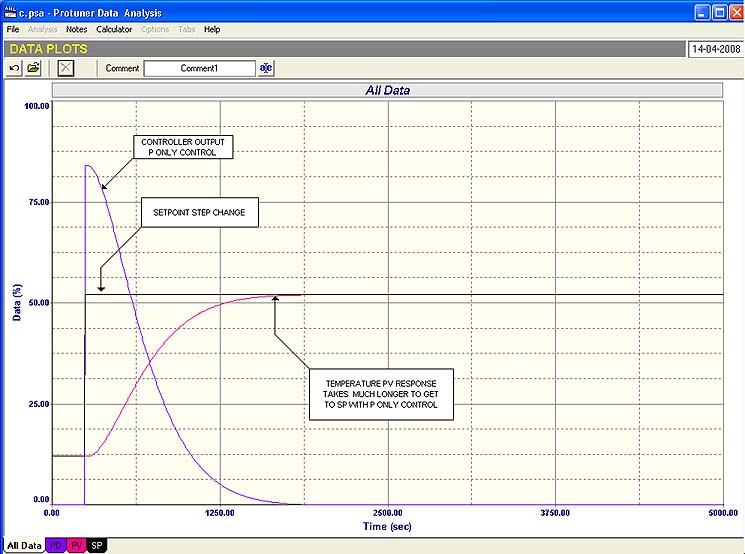
The results of such a tune with P and D is shown in Figure 3. Compare this with the Figure 4, which shows the best response you can get on this process using a P only control. It takes almost twice as long to get the process to setpoint.
Fig. 4
Just out of interest, it is extremely simple to control a process like this with P only control. If you think of it, and referring back to the drawing in Figure 1, you can see that it is impossible for the process to ever settle out below setpoint. This is due to the fact that the balance point is zero (valve is shut), so if the valve is even slightly open the temperature will rise. Therefore when the process is below setpoint, there will be a control error causing the valve to open, and the valve can only really shut fully when the process reaches setpoint where the error is zero. So the trick is with P only control to ensure that the P gain is just sufficient to get the process to setpoint as fast as possible without overshoot.
I think this is a very interesting process, which at first sight looks extremely difficult to tune, but is in fact very simple, if you have the necessary knowledge. As I also tell people on my courses:
“The only true magic in this learning is gaining understanding. Knowledge is power.”