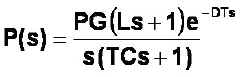Home About us Contact us Protuner Loop Analyser & Tuner Educational PDFs Loop Signatures Case Histories
Michael Brown Control Engineering CC
Practical Process Control Training & Loop Optimisation
Loop Problem Signatures Part 2 - 20
DYNAMICS OF MORE COMPLEX PROCESSES
POSITIVE LEAD INTEGRATORS - PART 1
Positive lead integrators are probably the most interesting of all the different dynamics you will ever come across, and normally the most rewarding, as you can often achieve spectacular improvements in loop performances when you tune them. Most loops that one comes across with such dynamics are usually terribly poorly tuned, with most of them reacting extremely slowly to changes. In some cases, correct tuning can improve response by several thousand times! Really dramatic stuff!
The Dynamics
Where L>>1 and L>>TC
PG = Process gain
L = Lead in seconds
DT = Deadtime in seconds
TC = Time constant in seconds
s is the Laplace Operator
The Response to a Step Change in Manual
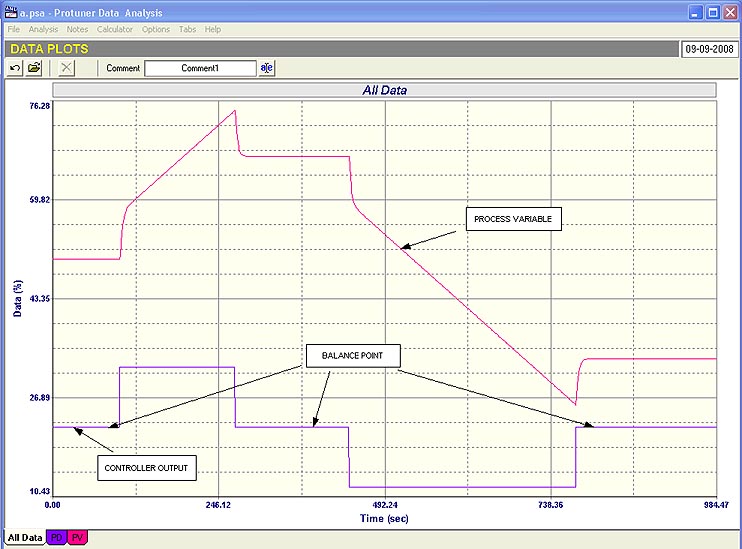
The response to step changes in the controller’s output is shown in Figure 1.
Fig. 1
It can be seen how the lead gives the PV an initial kick before the response settles into the normal ramp that is always associated with integrating processes. This kick makes life extremely difficult for operators if they have to run with the controller in manual. They already have problems trying to balance integrating process in manual. Now the kick increases the problems dramatically, as it appears that the process is running away even faster, and it makes it very difficult for them to get the process balanced at a particular value.
Where do You Find Positive Lead Integrators?
When I first got into the optimisation scene I was told that the place where one would probably only see positive lead integrator dynamics was on paper machine drier pressure control systems. This by the way, is a very important application, and is worth discussing in some detail.
Moisture and basis weight are amongst the two most important controls on a paper machine. The former controls the amount of water, and the latter controls the amount of pulp that one puts into the paper. Apart from other considerations like paper strength, water is cheaper than pulp so there are also powerful economic advantages in keeping these variables under tight control, and adding as much water as allowable in the paper recipe.
The moisture is varied by passing the paper over a large number of rollers in the paper machine, which are heated by passing steam through them. In actual fact the drier sections on a paper machine make up for a considerable amount of the bulk on these impressive and enormous machines, which can stretch a couple of hundred of meters in length.
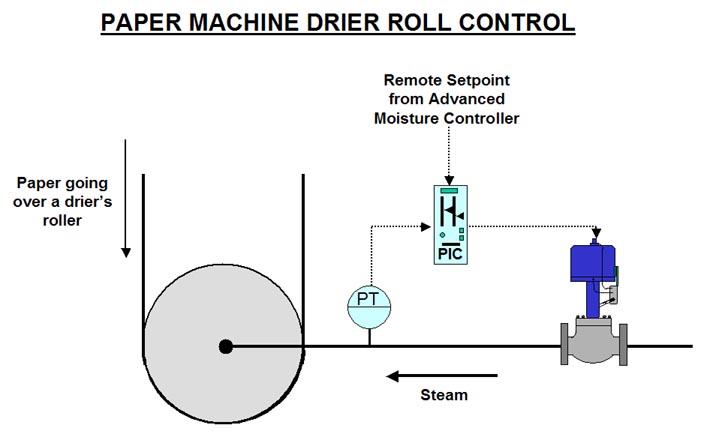
Modulating the internal pressure of the roller controls the drying effect of individual roller sections. A control loop is illustrated in Figure 2. When a step change is made on the controller’s output a positive lead effect is seen on the process variable (pressure signal) due to the effects on the steam saturation.
Fig. 2
It should be noted that the actual moisture in the paper is measured just as the paper leaves the machine and before it is wound up into a huge roll of paper called a jumbo. A travelling head that moves backwards and forwards on a yoke across the width of the paper performs the measurement of things like moisture and basis weight. These measurement techniques employ very sophisticated technology, some of which originated in space technology research.
The moisture signal is fed into an advanced control computerised system which takes all sorts of variables into account and eventually sends a signal to the setpoints of each of the individual roll sections’ steam pressure controllers on the base layer. It is important to note is that the requirement of this control system is for the steam pressure to follow setpoint as quickly as possible, with minimum control variance. It should also be noted that the setpoints do not change extremely quickly or in a step fashion, but tend to ramp around reasonably slowly.
Apart from this application, I soon discovered that positive lead integrators “pop-up” quite frequently in all sorts of situations, some of which are quite unexpected. A good example of this was on a control loop where I would have least expected it, and this was a density control loop in a plant in a coal mine where stones are separated from the coal, by the use of a dense liquid medium.
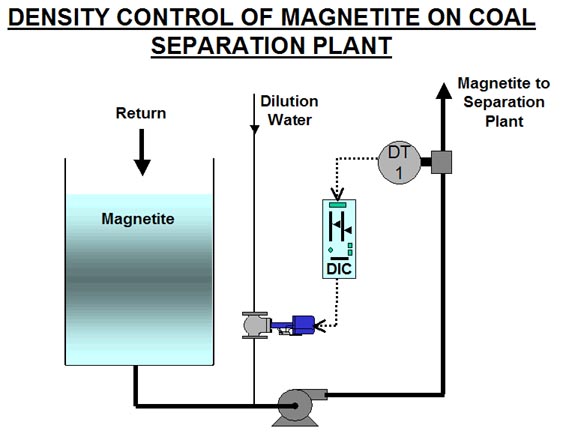
Figure 3 shows the process and control system exactly as it was drawn for me on arrival at the plant. The liquid in the tank is a magnetite solution. It is pumped up to the separation plant via a density transmitter. Dilution water is added on the pump suction side to control density. Now this at first site is obviously a self-regulating process. If the controller is in manual and if a step change is made on its output so as to increase the flow of dilution water, then surely one must expect the density to decrease to a certain point and then remain constant there? However on actually performing such a test, I was amazed to find that after an initial fast drop, the density then continued to decrease in a steady, constant downwards ramp.
Fig. 3
This is an excellent example of why it is so important for a person performing optimisation to really find out all the facts about the process, before trying to do tuning. After further talks with the process people, and a walk around the plant, I discovered that the magnetite in fact is recovered after the separation process and is then returned to the vessel. Therefore there is an initial decrease in density after the dilution water is increased, and then the returning, but now less dense liquid, once again passes through the pump, which is why it carries on ramping downwards. So it is in fact an integrating process. I will refer to this particular example later in the second part of this article, as it really does help one understand the workings of this particular dynamic response.
Some other examples of where I have encountered positive lead integrators are:
- 1. Level controls on cryogenic liquids.
- 2. Temperature controls where there is an initial fast rise in the temperature, followed by a ramp as the ambient in the area being heated starts to rise. Examples of this are on soaking pits in the steel industry, and in quite a few temperature control situations in petrochemical plants.
- 3. Level controls on small vessels with a small retention time, and with a control valve that has too much gain in the positioner, causing an overshoot on step changes.
- 4. Density controls on other dense medium separation plants in mining industries like the diamond mines.
It is important to always be on the lookout for the positive lead response on integrating processes, because as mentioned above, they crop up quite frequently, and sometimes very unexpectedly.
Correct tuning of positive lead integrating processes is very interesting as will be seen in the second part of this article. Positive lead integrators are extremely difficult to tune properly if one doesn’t understand this type of dynamics and how to deal with it. As very few people have ever been taught the facts behind these dynamics, the vast majority of these loops are terribly badly tuned, with an extremely slow response to changes. This is because of the positive lead, which tends to make people feel that the process has a tendency to “run away” very quickly, so they tune them very slowly so that changes are slow.
In Part 2 of this article which will be published in two months time, I will explain how these dynamics operate and show the correct method of tuning them.